擁抱「資料結構」的「演算法」(14) - 圖形 Graph
前言
說到圖形你會想到什麼呢?四邊形、五邊形還是長條圖、圓餅圖?圖形涵蓋的範圍非常的廣,而今天要討論的圖形指的是資料結構的其中一種,就讓我們一起來認識認識吧
生活常識
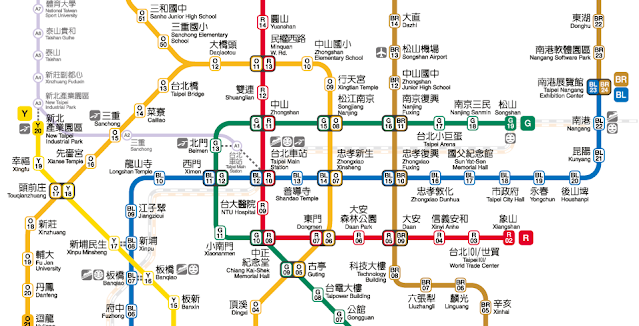
你有搭乘捷運或火車的經驗嗎?如果到了一個陌生環境,路線圖就會是你的好幫手,可以快速瀏覽目前所在位置與目的地之間的關係,而觀察下圖,會發現是由點與線所組成,每個車站都是一個點,並且會與相鄰的車站連線,例如,與台北車站相鄰的有:中山、善導室、臺大醫院、西門,這些站點跟台北車站之間都有連線
另外我們在使用交友軟體時,常常發現朋友之間還有許多共同朋友,而每個人都可以看成一個點,有成功建立朋友關係的人,他們之間則會存在連線,這就很像是我們的人脈網路圖
圖片來源:freerangestock
最後,生活中常看到的電線桿與電線也扮演著重要角色,讓整個城市都佈滿電力,其實也存在著點與線條的關係
圖片來源:https://www.pexels.com/zh-tw/photo/3881918/
專業知識 - 圖形 Graph
圖形定義
由上述的生活例子得知,有些圖形是由點與線條所組成,而資料結構的圖形也是類似的概念,是由頂點(Vertice)與邊(Edge)所組成,所以我們會使用 G = (V, E) 來定義一個圖形
G = ( V, E )
- G : 圖形(Graph)
- V : 所有頂點(Vertice)的集合
- E : 所有邊(Edge)的集合
圖形種類
- 無向圖(Undirected Graph):
邊不具有方向性,例如雙向道,或像是先學畫畫再學書法,也可以學書法再學畫畫都可以,邊以( A , B )表示
- V : { A, B, C, D, E }
- E : { ( A, B ), ( A, C ), ( B, C ), ( B, D ), ( C, D ), ( C, E ), ( D, E ) }
- 有向圖(Directed Graph):
邊具有方向性,例如單向道,或是像一定要讀完小學才能讀國中,邊以< A , B >表示
- V : { A, B, C, D, E }
- E : { < A, C >, < B, A >, < B, C >, < B, D >, < C, D >, < C, E >, < D, E > }
專有名詞
- 完整圖形(Complete Graph)
在無向圖中有 5 個頂點,若存在 10 個邊,符合公式:n ( n - 1 ) ÷ 2
在有向圖中有 5 個頂點,若存在 20 個邊,符合公式:n ( n - 1 )
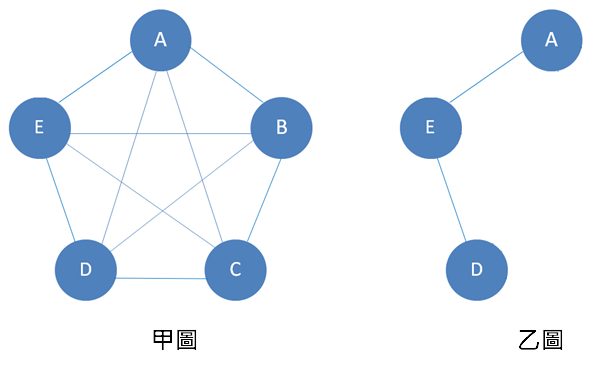
子圖 (Subgraph)
假設乙圖是甲圖的子圖,則乙圖的頂點會包含在甲圖的頂點集合中,且乙圖的邊也會包含在甲圖的邊集合中,路徑 (Path)
兩個頂點所經過的邊,稱為路徑,如上面乙圖的 A 到 D ,路徑為 { ( A, E), ( E, D ) }即為一條路徑路徑長度 (Path Length)
路徑上總共包含幾條邊,如上面乙圖的 A 到 D ,路徑為 { ( A, E), ( E, D ) },經過2條邊簡單路徑(Simple Path)
一條路徑中,起點與終點可以為同一個點,但其他頂點皆為不相同的點,不可重複出現
例如 A B C D E A 為簡單路徑,其中 A 為終點與起點,所以可以重複
例如 A B C D B A 不是簡單路徑,其中的 B 出現 2 次循環 (Cycle)
起點與終點為同一個頂點的簡單路徑,例如 A B C D E A,其中 A 為終點與起點相連
兩個頂點之間,存有路徑可以相通相連單元(Connected Components)
Components 有元件的意思,在無向圖中,代表圖形中有不同的元件,而元件指的不是頂點,也不是邊,而是指這個圖形是由多個子圖而組成,子圖與子圖之間不相連,但子圖的內部任一端點都存在路徑可以通往任一端點,如下圖,A、B、C中任一端點都可以存有路徑可到其他端點,而 D 與 E 之間也存有路徑,但左圖的 ABC 與右圖的 DE 之間並不存在路徑,所以下圖是由 2 個相連單元所組成強相連 (Strongly Connected)
在有向圖中,任意兩頂點彼此之間存在路徑可以互通,如下圖,A 點可以到 B 或 C 點,B 點可以到 A 或 C 點,C 點也可以到 A 或 B 點強相連單元(Strongly Connected Components)
在有向圖中,任意兩頂點彼此之間不存在路徑,例如 A 可以透過路徑 B C 到 E,但 E 卻沒有路徑可以到 A,則代表下圖不是強相連,且其中包含了強相連單元
強相連單元:分支度(Degree)
在無向圖中:
一個頂點含有幾個邊在有向圖中:
入分支度(In-Degree):箭頭指入此端點的個數,如下圖 A 的入分支度為 1
出分支度(Out-Degree):箭頭由此頂點指出的個數,如下圖 A 的出分支度為 2
今日小結
圖的專有名詞頗多,需要花一點時間理解一下,明天再來講圖形的表示法
今日謎題
在神密的麥田上,被刻畫了好幾個英文字母,並留下了這些訊息,請問你能從中觀察到什麼神秘訊息嗎?
- V : { W, B, C, D, E }
- E : { ( W, B ), ( B, D ), ( D, E ), ( E, C ), ( C, W ) }
昨日解謎
謎題說明:後序式讀取順序為由左往右,讀取資料的規則為連續 2 個數字與 1 四則運算就開始計算
計算過程
93 100 * 10 14 * + 13 +
一開始會先讀取到93 100 \*,電腦就會進行 93 * 100 = 9300 的運算9300 10 14 * + 13 +
接著會讀取到9300 10 14,但不符合連續 2 個數字與 1 四則運算的規則,所以繼續讀到10 14 \*,電腦就會進行 10 * 14 = 140 的運算9300 140 + 13 +
然後繼續由右往左讀取9300 140+,電腦就會進行 9400 + 140 = 9540 的運算9440 13 +
最後電腦就會進行 9440 + 13 =9453的運算
所以小美想聽的就是玖壹壹演唱的 9453,你答對了嗎?













留言
張貼留言